Veri setinde linear bir artış söz konusu ise bu veri üzerinde linear regression algoritması kullanılması tavsiye edilir. Örneğin Maaş – Zam, Yıla göre artış azalış gösteren veriler olabilir.

Elimizde bir x ve y birbirleriyle ilişkili değerler olsun. Bu değerler arasındaki ilişki bir koordinat düzleminde bir line ile çizdirebiliyorsanız tahmin etmek istediğiniz x değerine ilişkin y değerini rahatlıkla bulabilirsiniz.

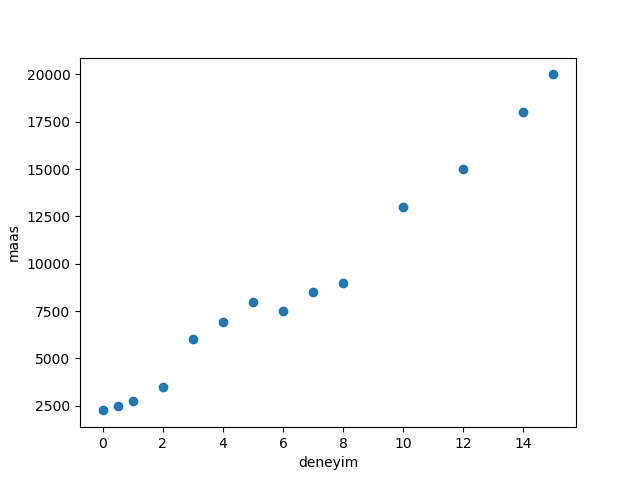
Örnek olarak Yukarıdaki veri setiyle bir işlem yapalım. Bir grafik çizdirdiğimizde deneyim ve maaş arasındaki ilişkiyi çıkarmaya çalışalım. Bu ilişki arasında öyle bir line fit çizelim ki bundan sonraki değerlerde de bu cevabı kullanalım.

Formül : y = b0 + b1*x -> b0 = constant (bias) -> Başlangıç değerim b1 = coeffiencient(Katsayım)

b0 = y noktasını kestiği kısım

b1 = Eğim -> a/b

bu örnek için maas = b0 + b1 * deneyim olacak.

residual = y – y_head (y_head predict edilen değerdir. y ise koordinat düzleminde y ‘e karşılık gelen kısımdır.)

Her nokta için residual değerleri hesaplanır. burada – değerlerini artı yapmak için şu işlem yapılır.

tüm sayılar için toplama yapılır => sum(residual*residual(kare))/14 buna da MSE Min Square Error denir.

Min Square Error ne kadar düşük olursa koordinat düzlemindeki elimizdeki verilere karşılık gelen bir line çizildiğinde en uygun şekilde yeni değerlerde tahminlemeler yapılacaktır.

# -*- coding: utf-8 -*-
import pandas as pd

import matplotlib.pyplot as plt

df = pd.read_csv("linear_regression_dataset.csv", sep = ";")

plt.scatter(df.deneyim,df.maas)
plt.xlabel("deneyim")
plt.ylabel("maas")
plt.show()

#%% sklearn

# Sklearn -> Machine Learning algoritmalarını içerisinde barındıran kütüphanedir.

from sklearn.linear_model import LinearRegression

# linear regression class 'ını bir linear_reg değişkenine atadık
linear_reg = LinearRegression()

x = df.deneyim.values.reshape(-1,1)
y = df.maas.values.reshape(-1,1)

#sklearn (14,) bir yapıyı anlamaz. Bunu (14,1) olarak güncellemeliyiz. -> reshape(-1,1) ile yaptık.


linear_reg.fit(x,y)

#%%

b0 = linear_reg.predict([[0]])
print("b0 : ", b0)

b0_ = linear_reg.intercept_
print("b0_: ",b0_)

b1=linear_reg.coef_
print('b1: ',b1)

# y ekseninin kestiği nokta, intercept --> 1663.8951 --> b0_
# egim ( slope ) --> 1138.3481 ---> b1


#%%
# visualize line 
y_head=linear_reg.predict(x)
plt.scatter( x , y )
#if we plot this line in red we see the following output
plt.plot( x, y_head , color='red')
plt.show()

Yukarıdaki veride artık her yeni x ve y değeri için çıkıcak sonuçları bilebiliriz.

# salary = 1663 + 1138 * experience

maas_yeni = 1663.89519747 + 1138.34819698 * 12
print(maas_yeni)

print(linear_reg.predict([[12]]))

Örnek olarak yukarıdaki gibi bir predict yapabiliriz.

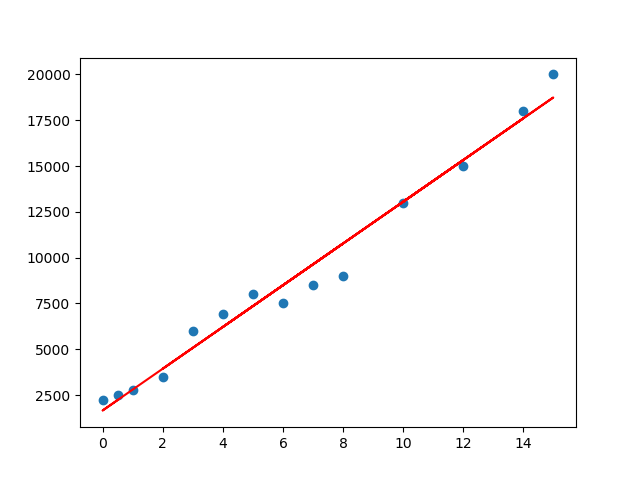
Son olarak line fit ‘i çizdirdiğimizde en doğru line yukarıdaki gibi olacaktır.